

We extended a fundamental principle in statistical mechanics called microscopic reversibility to the quantum world and experimentally verified it. Just appeared in PRL and selected as an Editor’s Suggestion and for a Synopsis in Physics.
The second law of thermodynamics states that the entropy of an isolated system tends to increase. But statistical mechanics shows that transient reductions in entropy can occur with a tiny probability. Central to the theorems that describe these fluctuations is microscopic reversibility—the idea that the probability of a system taking a specific trajectory through phase space is related to the probability of it taking the time-reversed version of that trajectory. Now we have demonstrated a quantum version of this principle.
The concept of microscopic reversibility must be adjusted when entering the quantum realm because of a key difference between classical and quantum phase spaces. Namely, the uncertainty principle prevents the position and momentum of quantum systems from being measured precisely at the same time. Additionally, the phase-space trajectories of such systems are affected by quantum coherence. Taking these factors into account, we considered a quantum system interacting with a thermal bath and derived a relation between the probabilities for a phase-space trajectory and its time-reversed version.
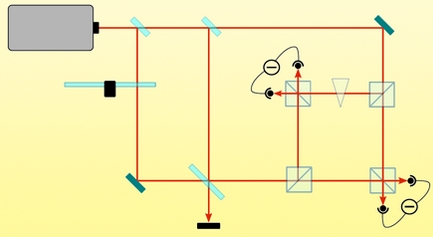
We experimentally demonstrated quantum microscopic reversibility using a simple optical setup in which laser light was mixed with the light from a thermal bath. We found that the derived probability relation accurately predicted our experimental results and that quantum effects were important only when the temperature of the thermal bath was low. By raising this temperature, we observed a transition from quantum to classical microscopic reversibility.


